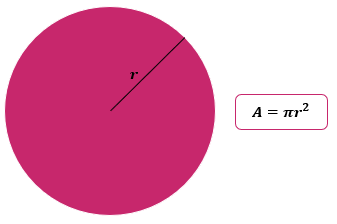Las figuras planas son aquellas que están limitadas por líneas rectas o curvas, además de que todos sus puntos están contenidos en un solo plano, es decir, no tienen relieve y sólo tienen dos dimensiones. Este tipo de figuras se dividen en polígonos (unión de líneas rectas) y cónicas (unión de líneas curvas).
Las figuras planas pueden ser regulares o irregulares. Nuestro estudio se centrará en las figuras regulares, es decir, aquellas cuyos ángulos y lados son iguales.
Área de figura plana
La medida de las superficies de las figuras planas, en geometría se denomina generalmente como área. El área, comprende la superficie o extensión dentro de una figura, lo cual se expresa en unidades de medida que denominamos superficiales. Veremos entonces aquí de que forma calcular el área de figuras planas, tales como el triangulo, cuadrado, rectángulo, etc.
Triángulo
El triángulo es un polígono el cual está formado por tres lados y tres ángulos, la suma de sus tres ángulos es de 180º. Para calcular el área de un triangulo, sin importar si es equilátero isósceles o escaleno, lo que debemos hacer es multiplicar la base por la altura y luego dividir esto entre dos.
Cuadrado
El cuadrado es un polígono que tiene sus cuatro lados iguales así como sus ángulos, que son todos rectos, la suma de ellos es de 360º. El área de un cuadrado es igual al valor de un lado multiplicado por si mismo. Pero conviene denominar base al lado horizontal y altura al lado vertical.
Fuente: Elaboración propia
Rectángulo
El rectángulo es un polígono de cuatro lados. Sus lados son iguales dos a dos. Los ángulos al igual que en el cuadrado son todos iguales y rectos. Para hallar el área de un rectángulo se permite establecer que la forma de calcular su superficie es igual a la del cuadrado. Siendo así su área:
Rombo
El rombo es un polígono de cuatro lados iguales, pero con los ángulos iguales dos a dos, dos obtusos y dos agudos. El área de un rombo es igual al producto de la diagonal mayor (D) por la diagonal menor (d) y el resultado de esto se divide entre dos. Veamos entonces:
Trapecio
El trapecio es un polígono de cuatro lados, dos de ellos paralelos. Sus cuatro ángulos son distintos de 90º, y la suma de estos es de 360 grados. Para hallar el área de un trapecio se suman las dos bases (b y B) y se multiplica por la altura (h) por último se divide entre dos. Observemos lo siguiente:
Vale decir que el área de un trapecio es nada más que la suma de uno de los pares de triángulos que se forman al trazar una diagonal. Por lo tanto la base mayor es la base de uno de los triángulos y la base menor la base del otro.
Paralelogramo
El paralelogramo es un polígono de cuatros lados que son iguales y también paralelos, dos a dos. Sus ángulos son distintos de 90 grados. Su superficie es igual al producto de la base por la altura. Veamos la siguiente representación:
Polígonos regulares
Los polígonos regulares son aquellos que tienen más de cuatro lados iguales, al igual que sus ángulos. El de cinco lados se denomina pentágono, el de seis lados hexágono, etc. Si queremos calcular el área de estos polígonos se debe multiplicar el perímetro (P) por la apotema (a) y luego esto dividirlo entre dos. Veamos ahora como sería la fórmula:
Circulo
Consideremos al círculo como un polígono regular cuyos lados son los puntos que conforman la circunferencia, lo cual sería su perímetro. Podemos decir entonces que El círculo es la región que está delimitada por una circunferencia, lugar geométrico de los puntos que equidistan en el centro. El círculo tiene un propiedad fundamental, que consiste en la relación permanente entre el radio y la medida de su circunferencia, el cual es un valor constante que denominamos con la letra griega PI, y su valor es de 3,1416. Para hallar el área de un círculo multiplicamos PI por el radio, elevado al cuadrado.